LEYES DE EXPONENTES

Las leyes de exponentes, o reglas de exponentes son varias. primero tenemos que entender que un exponente significa cuantas veces se debe multiplicar un número o una variable por si mismo. por ejemplo 4³, significa que el 4 debe multiplicarse 3 veces por si mismo, esto es : 4 · 4 · 4

Las tres primeras leyes

Las tres primeras leyes :

x¹ = x    Un numero elevado a la potencia 1, es siempre el mismo numero, es decir no cambia.

ejemplo:  3¹ =3

 x⁰ = 1   Cualquier numero elevado a la potencia 0 es siempre 1

 x^-1 = 1/x)  Cuando se tenga una potencia elevada a un numero negativo debe de "convertirse en positivo bajando todo el termino que este elevado a la potencia negativa a la posición del denominador o viceversa

ejemplo:

 x^-3 = 1/x³            1/x^-3 = x³ 

 4^-3 = 1/4³         1/4^-3 = 4³

4ta ley x^mxⁿ = x^m+n

Cuando se trata de la misma literal, los exponentes se suman. y los coeficientes se multiplican 

Ejemplo: 3x²·5x³ = 15x⁽²⁺³⁾ = 15x⁵

5ta ley  x^m/xⁿ = x^m-n

Cuando se trata de la misma literal , los exponentes se restan y los coeficientes se dividen

Ejemplo:  8x⁷/2x² =4x^7-2  = 4x⁵ 

8 entre 2 da 4 y lso exponentes se restaron quedando 7 menos 2 es igual a 5

6ta ley  (x^m)ⁿ = x^mn

Cuando se tiene un exponente elevado a otro exponente, los exponenntes se multiplican entre si. y los coeficientes se elevan 

Ejemplo: (5x³)² = 25x⁶

el coeficiente 5 es elevado a la potencia 2. esto es 5·5=25 y el exponente 3 es multiplicado por el exponente 2,    3·2=6

7ma ley (xy)ⁿ = xⁿyⁿ

Cuando existe una multiplicación dentro de un paréntesis y este esta elevado a alguna potencia, se realiza la multiplicación de los coeficientes Para ver cómo funciona, sólo piensa en ordenar las "x"s y las "y"s como en este ejemplo:

Ejemplo: (3x· 2y)³ = (27x³ · 8y³)= 216x³y³

           Se eleva cada coeficiente a la potencia 3, y los exponentes se multiplican. x tiene exponente a la 1 potencia que se multiplica por la potencia 3. Despues se multiplcan los coeficientes 27  por 8 nos da 216 y se le agregan las literales  216x³y³

8va ley (x/y)ⁿ = xⁿ/yⁿ

Cuando existe una fracción elevada a un exponente, primero  se dividen los coeficientes si es posible, y los exponentes se multiplican entre si. 

Ejemplo: (8x/2y)³ = (512x³/8y³)³ = 64x³/y³

el 8 y el 2 son elevados a la potencia 3 respectivamente, como resultado nos queda: 

(512x³/8y³)³ 

enseguida se procede a dividir el 512 entre 8, quedando como resultado final 

64x³/y³

9na  ley q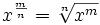 

Cuando existe una potencia elevada a una fracción, se puede representar o reescribir en forma de raiz. esto es el denominador de la potencia "denomina" el tipo de raizy el numerador queda como potencia del termino. 

Ejemplo: